Participant Proposed Plan

Proposal Title: Applications, Evaluation and Improvement of a Coupled, Global and Cloud-Resolving Modeling System

Principal Investigator: Dr. Wei-Kuo Tao

Goddard Laboratory for Atmospheres

NASA/Goddard Space Flight Center

Greenbelt, MD 20771

(301) 614-6269

email: tao@agnes.gsfc.nasa.gov

Co-Principal Investigator: Dr. Robert Atlas (NASA GSFC), Dr. Haoqiang H. Jin (NASA Ames)

Co-Investigators: Dr. J. Bacmeister, Dr. J. Chern, , Dr. A. Hou, Dr. W. Lau, A. Negri, Dr. W. Olson, Dr. D. Wang (NASA Langley), Dr. Z. Wang, Dr. M. Zhang (SUNY)

ABSTRACT

Recent GEWEX Cloud System Study (GCSS) model comparison projects have indicated that cloud-resolving models (CRMs) agree with observations better than traditional single-column models in simulating various types of clouds and cloud systems from different geographic locations. Current and future NASA satellite programs can provide cloud, precipitation, aerosol and other data at very fine spatial and temporal scales. Such programs require a coupled global circulation model (GCM) and cloud-scale model (termed a super-parameterization or multi-scale modeling framework, MMF) in order to use these satellite data to improve the understanding of the physical processes that are responsible for the variation in global and regional climate and hydrological systems. The use of a GCM will enable global coverage, and the use of a CRM will allow for better and more sophisticated physical parameterization. NASA satellite and field campaign cloud-related datasets can provide initial conditions as well as validation for both the MMF and CRMs.

The proposed research meets the requirements and addresses the scientific problems as stated in NN-H-04-Z-YS-008-N and particularly focuses on the Cloud Modeling and Analysis Initiative (CMAI). Here we will utilize NASA's satellite data and field campaign observations to extend our understanding of clouds and evaluate realistic impacts of clouds on climate and weather models. Cloud process models and a coupled global-cloud process modeling system can generate a cloud library and provide information on cloud and precipitation microphysical and dynamic processes as well as their interactions with radiation and aerosols.

A seed fund is available at NASA Goddard to build an MMF based on the 2D GCE model and the Goddard finite volume general circulation model (fvGCM). The purpose of this proposal is to augment the current Goddard MMF and other cloud modeling activities. The major objectives of this proposal are:

(1) To evaluate and identify the CRM's capabilities with the focus of improving the CRM as it relates to the MMF,

(2) To use NASA satellite data and field campaign observations to validate and improve the CRM used in the MMF,

(3) To produce and provide multi-dimensional cloud data sets (i.e., a cloud data library) to the global modeling community to help improve the representation and performance of moist processes in climate models and to improve our understanding of cloud processes globally (software tools needed to produce cloud statistics and to identify various types of clouds and cloud systems from both high-resolution satellite and model data will be developed jointly), and

(4) To enhance the computational performance of the MMF on NASA high performance super-computers. Computer scientists at NASA Ames will port, extend, and enhance the performance of the MMF and develop tools and methodologies, including visualization packages, to manage and display the immense data sets generated by the MMF.

Revised Yearly Plan (See Red for highlights – Priorities)

Task

Year 1

Year 2

Year 3

Task 1

Evaluation and Improvement of the MMF using Observational Data

Develop the cloud classification techniques

Implement ISCCP simulator into MMF

Conduct MMF experiments (1998, 1999 and 2000)

Start evaluating MMF for diurnal variation from different geographic regions and climate regimes

Develop the cloud classification techniques

Perform MMF sensitivity tests with explicit CRM-simulated surface processes and radiation

Evaluate MMF for various clouds/cloud systems from different geographic regions and climate regimes

Examine MMF-simulated diurnal variation and compare with satellite data (i.e., ISCCP)

Start developing the MMF interface to support global bands of the 2D GCE

Conduct MMF experiments with global bands of the 2D GCE model

Examine the impact of MMF-CRM simulated surface and radiation processes on the diurnal variation of clouds and precipitation

Continue evaluating the MMF performance using NASA satellite data

Task 2

Production of Cloud Library

Begin producing four-dimensional cloud datasets (i.e., SCSMEX, ARM and KWAJEX) and compare simulated results with observed (i.e., from field campaigns) – a cloud library will be available on a Goddard Web site

Perform GCE/WRF simulations for CRYSTAL-FACE and IHOP

Begin preliminary comparisons between GCE-simulated cloud and precipitation properties and those retrieved from satellite observations.

Test the coupled CRM with Eddington forward radiative transfer and spaceborne radar and lidar models

Begin preliminary comparisons between CRM-simulated and observed radiances, reflectivities, and attenuation using TMI, AMSR-E, and PR data

Continue producing cloud datasets and coordinate with DIME regarding quality checking, product definition, reformatting, and archiving of datasets

Couple GCE and reverse Monte Carlo model to obtain more accurate radiance simulations

Continue comparisons between GCE-simulated clouds and precipitation properties and GCE-simulated radiances, reflectivities, and attenuation against those derived from observations

Coordinate and determine the types of cloud datasets useful for parameterization developers

Continue evaluating CRM/WRF results with observations from ground-based and satellite observations

Use calibrated CRM/WRF to produce “cloud library” for science community

Test improvements to the GCE model physical parameterizations using observational data

Task 3

Improve the MMF computational performance

Optimize serial performance of the 2D GCE code and demonstrate performance improvement on the Columbia supercomputer

Improve the hybrid MPI+OpenMP version of MMF so that the 2D GCE codes are properly coupled into calculations at each grid point of fvGCM

Scale this version up to 256-512 processors of a Columbia node

Demonstrate continuing performance improvement of the hybrid MMF across multiple Columbia nodes

Develop a 2D domain decomposition strategy for the simple MMF framework with 2D GCE cyclic lateral boundary conditions

Compare approaches using both pure MPI and a combination of MPI and OpenMP

Apply load balancing techniques in coupling the global GCE with fvGCM and compare performance with other approaches

Demonstrate the use of the multi-view display technology on MMF and cloud library datasets.

Investigate the capability of the distributed component architecture for remote access of MMF/cloud library datasets

Cloud-Precipitation Parameterizations in GCE model, Goddard MMF and WRF

Description of the GCE Model and Its Microphysical Schemes

The Goddard Cumulus Ensemble (GCE) Model, a CRM, has been developed and improved at NASA/Goddard Space Flight Center over the past two decades. Improvements and testing were presented in Tao and Soong (1986), Tao et al. (1989), Tao and Simpson (1993), Ferrier (1994), Tao et al. (1996), Wang et al. (1996), Lynn et al. (1998), Baker et al. (2001) and Tao et al. (2003). A review on the application of the GCE model to the understanding of precipitation processes can be found in Simpson and Tao (1993) and Tao (2003).

One of the unique characteristics of the GCE model is its microphysical process (Table 1). The cloud microphysics includes a parameterized Kessler-type two-category liquid water scheme (cloud water and rain), and a three-category ice-phase scheme (cloud ice, snow and hail/graupel) mainly based on Lin et al. (1983) and Rutledge and Hobbs (1984). The following major improvements have been made to the model during the past several years: (i) the addition of a two-moment four-class ice scheme (Ferrier 1994; Ferrier et al. 1995), and (ii) the addition of two detailed, spectral-bin models (Khain et al. 1999, 2000; Chen and Lamb 1999). These new microphysics require the multi-dimensional Positive Definite Advection Transport Algorithm (MPDATA, Smolarkiewicz and Grabowski 1990) to avoid "decoupling" between mass and number concentration[1].

McCumber et al. (1991) have tested the impact of warm rain only (no ice), two class ice and two different three-class ice schemes on the development and organization of a GATE squall line. Only newer improvements (three-class ice schemes, four-class ice scheme, and spectral bin microphysics) will be described.

	Characteristics	References
Warm Rain	qc, qr	Kessler (1969), Soong and Ogura (1973)
2 Ice	qc, qr, qi, qg	Cotton et al. (1982), Chen (1983), McCumber et al. (1991)
3Ice - 1	qc, qr, qi, qs, qh	Lin et al. (1983), Tao and Simpson (1989, 1993)
3Ice - 2	qc, qr, qi, qs, qg	Rutledge and Hobbs (1984), Tao and Simpson (1989, 1993)
3Ice - 3	qc, qr, qi, qs, qh	Lin et al. (1983), Rutledge and Hobbs (1984), Ferrier at al. (1995)
3Ice - 4	qc, qr, qi, qs, qg or qh	Lin et al (1983)
3Ice - 5	Saturation Technique	Tao et al. (1989), Tao et al. (2003), Lang et al. (2006)
4Ice - 1	qc, qr, qi, qs, qg, qh Ni, Ns, Ng, Nh	Ferrier (1994) Ferrier et al. (1995)
4Ice - 2	qc, qr, qi, qs, qg, qh Ni, Ns, Ng, Nh	Tao et al. (2002a)
One-Moment Spectral - Bin	43 bins for 6 types of ice, liquid water and cloud condensation nuclei	Khain and Sednev (1996), Khain et al. (1998)
Multi-component Spectral - Bin	Liquid: 46 bins for water mass, 25 for solute mass Ice: water mass, solute mass, aspect ratio	Chen and Lamb (1994, 1999)

Table 1 The microphysical schemes that have been implemented (coded) and tested in the GCE model.

(a) Three-Class Ice (3ICE) Scheme

A two-class liquid and three-class ice microphysics scheme (Fig. 2) developed and coded at Goddard (Tao and Simpson 1993) was mainly based on Lin et al. (1983) with additional processes from Rutledge and Hobbs (1984). However, the Goddard microphysics scheme has several modifications. The modifications include: (1) the option to choose either graupel or hail as the third class of ice (McCumber et al. 1991). Graupel has a low density and a large intercept (i.e., high number concentration). In contrast, hail has a high density and a small intercept (low number concentration). These differences can affect not only the description of the hydrometeor population, but also the relative importance of the microphysical-dynamical-radiative processes. (2) the saturation technique (Tao et al. 1989): This saturation technique is basically designed to ensure that supersaturation (subsaturation) cannot exist at a grid point that is clear (cloudy). This saturation technique is one of the last microphysical processes to be computed. It is only done prior to evaluating evaporation of rain and snow/graupel/hail deposition or sublimation. (3) Another difference is that all microphysical processes (transfer rates from one type of hydrometeor to another) that do not involve melting, evaporation and sublimation, are calculated based on one thermodynamic state. This ensures that all these processes are treated equally. The opposite approach is to have one particular process calculated first modifying the temperature and water vapor content (i.e., through latent heat release) before the second process is computed.

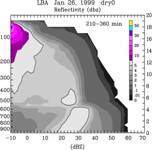
The conversion of cloud ice to snow in the 3ICE schemes was also recently modified to reduce over-estimated and unrealistic graupel amount in the stratiform region. Various assumptions associated with saturation technique were also revisited and examined (Tao et al. 2003). Recently, Lang et al. (2006) have simulated two types of convective cloud systems that formed in two distinctly different environments observed during the Tropical Rainfall Measuring Mission Large-Scale Biosphere–Atmosphere (TRMM LBA) experiment in Brazil. Model results showed that eliminating the dry growth of graupel in the Goddard 3ICE bulk microphysics scheme effectively removed the unrealistic presence of high-density ice in the simulated anvil. However, comparisons with radar reflectivity data using contoured-frequency-with-altitude diagrams (CFADs) revealed that the resulting snow contents were too large (Fig. 1, middle panel). The excessive snow was reduced primarily by lowering the collection efficiency of cloud water by snow and resulted in further agreement with the radar observations. The transfer of cloud-sized particles to precipitation-sized ice appears to be too efficient in the original scheme. Overall, these changes to the microphysics lead to more realistic precipitation ice contents in the model (see Fig. 1). However, artifacts due to the inability of the one-moment scheme to allow for size sorting, such as excessive low-level rain evaporation, were also found but could not be resolved without moving to a two-moment or bin scheme. As a result, model rainfall histograms underestimated the occurrence of high rain rates compared to radar-based histograms. Nevertheless, the improved precipitation-sized ice signature in the model simulations should lead to better latent heating retrievals as a result of both better convective-stratiform separation within the model as well as more physically realistic hydrometeor structures for radiance calculations.

Fig. 1 Reflectivity CFADs for the 26 January 1999 case derived from (a) observed S-pol radar reflectivity data, (b) the simulation using control microphysics, and (c) the simulation using control microphysics with no dry growth of graupel and reduced snow production.

(b) Two-Moment Four-Class Ice (4ICE) Scheme

An improved microphysical parameterization called 4ICE has been developed and implemented into the two-dimensional version of the GCE model (Ferrier 1994; Ferrier et al. 1995), which combines the main features of previous three-class ice schemes by calculating the mixing ratios of both graupel and frozen drops/hail. Additional model variables include the number concentrations of all ice particles (small ice crystals, snow, graupel and frozen drops), as well as the mixing ratios of liquid water in each of the precipitation ice species during wet growth and melting for purposes of accurate active and passive radiometric calculations. The scheme also includes the following: (1) more accurate calculation of accretion processes, including partitioning the freezing of raindrops as sources of snow, graupel and frozen drops/hail; (2) consideration of rime densities and riming rates in converting between ice species due to rapid cloud water riming; (3) incorporation of new parameterizations of ice nucleation processes, the rime splintering mechanism using laboratory data, and the aircraft observations of high ice particle concentrations; (4) shedding of liquid water from melting ice and from excessive amounts of water accumulated on supercooled frozen drops/hail; (5) preventing unrealistically large glaciation rates immediately above the freezing level by explicitly calculating freezing rates of raindrops and freezing rates of liquid water accreted onto supercooled ice; (6) introducing fall speeds and size distributions for small ice crystals; (7) calculating radar reflectivities of particles with variable size distributions and liquid water coatings from Rayleigh theory; (8) basing conversion of particle number concentrations between hydrometeor species on preserving spectral characteristics of particle distributions rather than conserving their number concentrations (important). A detailed description of these parameterized processes can be found in Ferrier (1994).

The 4ICE scheme was recently coupled with the MPDATA, substantially reducing the decoupling of mixing ratios and number concentrations caused by advection errors, resulting in a significant improvement in model performance. The 4ICE scheme has also been implemented into the three-dimensional version of the GCE model. The impact of the 3ICE or 4ICE scheme on the organization of two tropical squall systems was discussed in Tao et al. (2003a).

(c) Spectral-Bin Microphysics (Professor A. Khain, Hebrew University of Jerusalem)

The formulation of the explicit spectral bin-microphysical processes is based on solving stochastic kinetic equations for the size distribution functions of water droplets (cloud droplets and raindrops), and six types of ice particles: pristine ice crystals (columnar and plate-like), snow (dendrites and aggregates), graupel and frozen drops/hail. Each type is described by a special size distribution function containing 33 categories (bins). Atmospheric aerosols are also described using number density size-distribution functions (containing 33 bins). This model is specially designed to take into account the effect of atmospheric aerosols on cloud development and precipitation formation.

Droplet nucleation (activation) is derived from the analytical calculation of supersaturation, which is used to determine the sizes of aerosol particles to be activated and the corresponding sizes of nucleated droplets. Primary nucleation of each type of ice crystal takes place within certain temperature ranges. The rate of primary ice generation and freezing is calculated using a semi-lagrangian approach allowing one to calculate changes in supersaturation and temperature in moving cloud parcels attaining model grid points (Khain et al. 2000). Secondary ice generation is described by the Halett and Mossop (1974) mechanism, where, for every 250 collisions between droplets with radii exceeding 20 and graupel particles, one ice splinter is formed. Based on measurements, this process is assumed to occur within the -3 to -8 ^oC temperature range. The rate of drop freezing follows the observations of immersion nuclei by Vali (1975) and homogeneous freezing by Pruppacher (1995). Diffusion growth of water droplets and ice particles is calculated from analytical solutions for supersaturation with respect to water and ice. The shape of the ice crystals is accounted for in the calculation of diffusion growth for the different ice crystals. An efficient and precise method of solving the stochastic kinetic equation (Bott 1998) was extended to a system of stochastic kinetic equations calculating water-water, water-ice and ice-ice collisions. The model uses height-dependent drop-drop and drop-graupel collision kernels calculated from a hydrodynamic method valid within a wide range of drop and graupel sizes (Khain et al. 2001; Pinsky et al. 2001). Ice-water and ice-ice collision kernels are calculated taking into account the shapes of the ice crystals and the dispersion of terminal velocities for crystals of the same mass but different shape. Ice-ice collision rates are assumed to be temperature dependent. An increase in the water-water and water-ice collision kernels by the turbulent/inertia mechanism was taken into account following Khain and Pinsky (1997), Pinsky and Khain (1998) and Pinsky et al. (1998, 1999, 2000). The representation of collision-induced breakup of raindrops was also considered (Seifert et al. 2004). The model provides precipitation rates, accumulated rain, mass contents, total water and ice radar reflectivities, and mean and effective radii of droplets and ice particles. A detailed description of these explicitly parameterized processes can be found in Khain and Sednev (1996) and Khain et al. (1999, 2001).

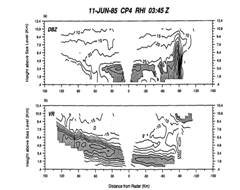
The explicit spectral-bin microphysics can be used to study cloud-aerosol interactions and nucleation scavenging of aerosols, as well as the impact of different concentrations and size distributions of aerosol particles upon cloud formation (see Fig. 2). The spectral-bin microphysics is expected to lead to a better understanding of the mechanisms that determine the intensity and the formation of precipitation for a wide spectrum of atmospheric phenomenon related to clouds. In addition, the spectral bin microphysics can be used to improve the GCE simpler bulk (3-class ice and two-moment four-class ice schemes) parameterizations.

Figure 2 Comparison of simulated vs. observed radar reflectivities for PRE-STORM (upper row), TOGA COARE (middle row), and CRYSTAL (lower row) cases. The left column is for clean conditions, the middle column dirty conditions, and the right column observations. The simulated radar reflectivities are instantaneous values at t=12 hours for the PRE-STORM and TOGA COARE cases and at t=3 hours for the CRYSTAL case. The observed PRE-STORM radar reflectivity pattern (upper right) is adapted from Fig. 5 in Rutledge et al. (1988) and shows the signature at 3:34 UTC on June 11, 1985. The TOGA COARE radar reflectivity observations (middle right) are plotted using airborne Doppler radar data collected at 21:16 UTC on February 22, 1993 (provided by David P. Jorgensen, Fig. 7 in Jorgensen et al. 1997). The CRYSTAL observations (lower right) show airborne EDOP radar data taken from 20:16 to 20:30 UTC on July 16, 2001 (courtesy of Gerry Heymsfield, NASA GSFC). The GCE model results indicate that an increase in CCN slowed precipitation processes for an Oklahoma squall line and an isolated and short-lived Florida cloud but significantly increased the rainfall for an oceanic tropical squall system

(d) Description of the multicomponent spectral bin model (Professor J.-P. Chen National Taiwan University)

The detailed cloud microphysical scheme to be coupled with the dynamic is based on the multicomponent microphysical model of Chen and Lamb (1994b, 1999), which allows simultaneous and independent changes of various physical and chemical properties of the cloud particles. For the proposed studies, two bin-components (water mass m_w and major solute mass m_s) are used for the liquid-phase framework and three bin-components (water mass, major solute mass, and aspect ratio--defined as the ratio of c-axis length to a-axis length) for the ice-phase framework. Forty-six bins are used for the water-mass component, 25 for the major solute component and 11 for the aspect ratio component. The lower bin-limits of successive smaller bins are defined as m_i = m_i+1 / q_i+1, where q is the bin-sizing factor. It is sometimes desirable to have higher resolution at a particular range of the bin spectrum. For instance, the accuracy of the numerical scheme applied here is more sensitive to the collection processes, which are more important for the larger particles. Therefore, we applied a variable bin-sizing factor so that qi = q·q_i+1, where q is a constant greater than unity for both the water and solute components. Note that the ranges for the first and last bins are extended to cover extreme conditions, so m₁ and m_N+1 do not follow the above definition. In addition, all droplets that fall into the last water-mass bin (mass exceeding m_w,46) are allowed to breakup aerodynamically. A method-of-moments type scheme is used to conserve various physical and chemical properties of cloud particles for their redistribution within the particle framework due to various growth mechanisms.

Liquid-phase microphysical processes considered in the model are the activation of condensation nuclei into cloud drops, the subsequent condensational growth, and collision-coalescence and breakup. Ice-phase processes included are the heterogeneous deposition/condensation nucleation, heterogeneous freezing, contact freezing, homogeneous freezing, diffusional growth, accretional growth, rime-splintering, melting, shedding due to melting and wet riming, and the aggregation of snow crystals. Beside the acquisition of water and solute, the change of shape (aspect ratio) due to all these processes is also calculated explicitly following the parameterization scheme of Chen and Lamb (1994a). Aqueous-phase chemistry considered includes the absorption/desorption of NH₃, H₂SO₄, HNO₃, SO₂, O₃, H₂O₂, CO₂, their ionic dissociations, and the oxidation of sulfite by O₃ and H₂O₂. Ice-phase chemical processes included are the sorption/desorption of SO₂ and H₂O₂ onto ice surface as well as the entrapment of SO₂ inside the ice during riming.

The simultaneous consideration of water and solute mass contents allows this model to truly resolve the aerosol-cloud interactive processes, such as the size-dependent aqueous chemistry and the recycling of aerosols after cloud dissipation. Furthermore, this particle framework may take any type of aerosol size distribution for its initial conditions, either observed or parameterized. For most applications where observations of aerosol physical and chemical properties are not available, we will adopt the a trimodal log-normal distribution as suggested by Whitby (1978) or Jaenicke (1993) for different areas:

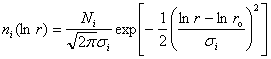
where N, r_o and s, are the total number concentration, modal value and standard deviation for each mode, respectively, and the subscript i = 1, 2, 3 represents the 3 modes. Because of all these features, this cloud microphysical model is in effect also an aerosol model.

Some modifications have been made since the Chen and Lamb (1994) version: For the microphysical processes, the more detailed formulas of Böhm’s (1992a, b) are used to calculate the fall speed and collision efficiencies of droplets; also, a hybrid coalescence efficiency that combines the experimental results of Low and List (1982) and Beard and Ochs (1984) is used to give a more complete cover of the size range. For the chemistry, nitric acid vapor and nitrate are included as additional gas-phase and aqueous-phase species. Some aerosol growth mechanisms are also considered in the latest version.

The major differences between the two detailed spectral-bin schemes are shown in the following table.

A. Khain